
In our case, one leg is a base, and the other is the height, as there is a right angle between them. To find the area of the triangle, use the basic triangle area formula, which is area = base × height / 2. For this special angle of 45°, both of them are equal to √2/2. If you know trigonometry, you could use the properties of sine and cosine.
In our case, this diagonal is equal to the hypotenuse.
As you probably remember, the diagonal of the square is equal to side times square root of 2, that is a√2. Again, we know that both legs are equal to a. Like the 30°-60°-90° triangle, knowing one side length allows you to determine the lengths of the other sides of a 45°-45°-90° triangle.Ĥ5°-45°-90° triangles can be used to evaluate trigonometric functions for multiples of π/4.As you know one leg length a, you the know the length of the other as well, as both of them are equal.įind the hypotenuse from the Pythagorean theorem: we have a² + b² = c² and a = b, soĭid you notice that the 45 45 90 triangle is half of a square, cut along the square's diagonal? The 45°-45°-90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°-45°-90°, follow a ratio of 1:1:√ 2. This type of triangle can be used to evaluate trigonometric functions for multiples of π/6. Then using the known ratios of the sides of this special type of triangle: a =Īs can be seen from the above, knowing just one side of a 30°-60°-90° triangle enables you to determine the length of any of the other sides relatively easily. 45°-45°-90° triangle: The 45°-45°-90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°-45°-90°, follow a ratio of 1:1. For example, given that the side corresponding to the 60° angle is 5, let a be the length of the side corresponding to the 30° angle, b be the length of the 60° side, and c be the length of the 90° side.: This type of triangle can be used to evaluate trigonometric functions for multiples of /6. Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratio. In this type of right triangle, the sides corresponding to the angles 30°-60°-90° follow a ratio of 1:√ 3:2. The 30°-60°-90° refers to the angle measurements in degrees of this type of special right triangle. The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation: A = Examples include: 3, 4, 5 5, 12, 13 8, 15, 17, etc.Īrea and perimeter of a right triangle are calculated in the same way as any other triangle. Equal sides are called lateral, and the last unequal side is called the base of the triangle. In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. An isosceles triangle is a triangle in which the two sides are equal in length. If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle. The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle. BASE OF ISOSCELES TRIANGLE CALCULATOR FREE
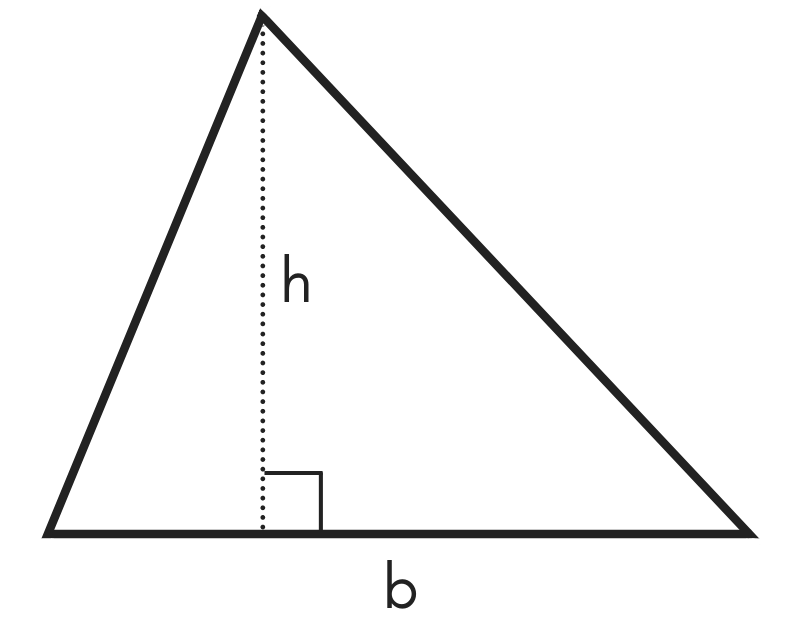
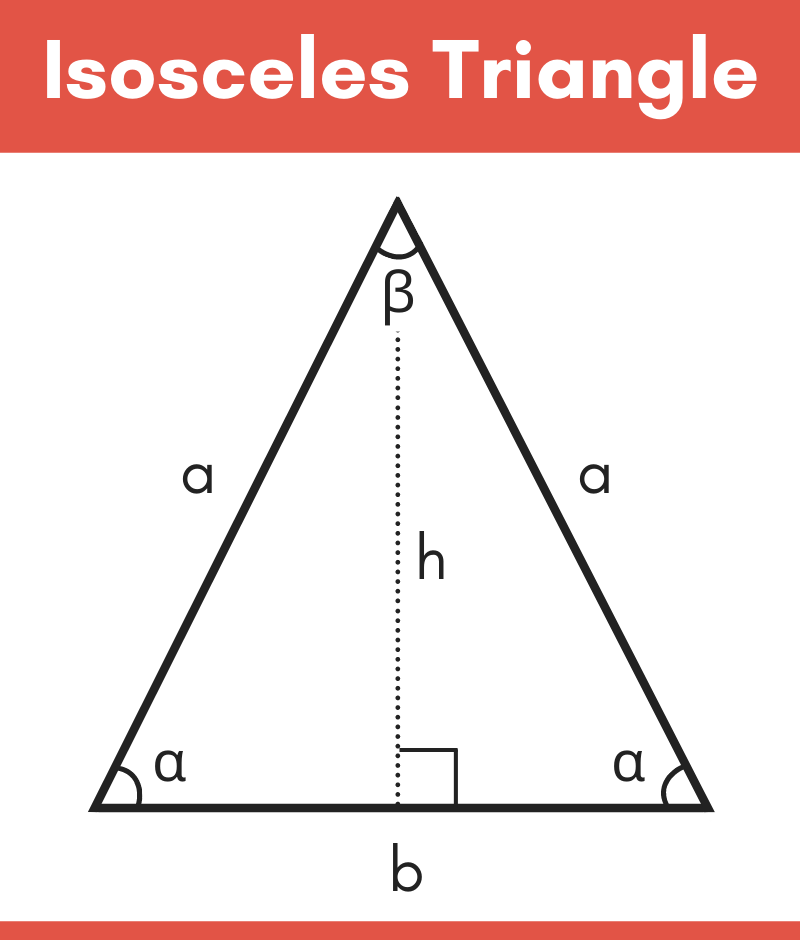
h refers to the altitude of the triangle, which is the length from the vertex of the right angle of the triangle to the hypotenuse of the triangle. This free triangle calculator computes the edges, angles, area, height, perimeter, median, as well as other values and a diagram of the resulting triangle. In this calculator, the Greek symbols α (alpha) and β (beta) are used for the unknown angle measures. Their angles are also typically referred to using the capitalized letter corresponding to the side length: angle A for side a, angle B for side b, and angle C (for a right triangle this will be 90°) for side c, as shown below.
The sides of a right triangle are commonly referred to with the variables a, b, and c, where c is the hypotenuse and a and b are the lengths of the shorter sides.

In a right triangle, the side that is opposite of the 90° angle is the longest side of the triangle, and is called the hypotenuse. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry. To calculate the properties of an isosceles triangle when given certain information, you can use the Pythagorean theorem, the Law of Cosines, or the Law of Sines. Triangle Calculator Pythagorean Theorem Calculator Right triangle A right triangle is a type of triangle that has one angle that measures 90°. An isosceles triangle is a triangle where two sides have the same length. Related Triangle Calculator | Pythagorean Theorem Calculator Right triangleĪ right triangle is a type of triangle that has one angle that measures 90°. This calculator calculates any isosceles triangle specified by two of its properties.







 0 kommentar(er)
0 kommentar(er)
